How will you explain ‘Blockchain’ to a 5-year old child?

Today we are going to try to understand what blockchain is from the perspective of a child. Something like this would be really helpful when you are approached by your little sibling. You wouldn't really have to sit and think before explaining it to them and trying so very hard to not utter something complicated. This would also be an exercise in understanding Blockchain in the simplest of terms with real-life analogies.

So without further ado… Let’s Begin.

To start our journey, let’s take four friends — Ravi, Alice, Wasim, and Bob. Each of them has chocolates with them (1 Eclairs and 3 Gems, don’t get greedy now!). They love going on adventures and we’ll see how they have gone on 4 such adventures. We would also help them solve their problems and learn what Blockchain is. Sounds right? Let’s get started.

The Mystery of the Missing Gem.

Now Ravi decides to share his yellow gem with Alice. As you can see below, he has given her the gem already. Now, Alice has 1 Eclair, and 4 gems while Ravi has 1 Eclair and only 2 gems.

But Alice is a bit greedy. She is hungry and decides to eat the gem that Ravi had given to her. Ravi has shared his gem with her but there is no proof of it. She decides to tell Wasim and Bob that she did not get Ravi’s gem. Ravi, on the other hand, has clearly shared his yellow gem. (Turn to the next page to see the current result).

Let’s take this as Problem 1.

Unknown Treasure Found!

How great would it be if we could go on adventures, right? Well, Bob in this pic has already gone on one and has found a treasure!

Now, remember how everyone started out with 1 Eclair and 3 gems each? Bob too had the same number gems. But he went on a quest and found a treasure chest. He discovered an extra gem and decided to use that as well.

But is this even right? How can Bob be allowed to have an unfair advantage? If Bob has done it, what’s stopping Alice or Wasim from using extra Eclairs that they might have found? So, we come to the conclusion that this cannot be allowed. But how can we prevent this from happening?

Let’s call it Problem 2.

The Double Eclairs Dilemma.

Again, let’s return to the initial point. Everyone had 1 Eclair and 3 gems. Now Alice and Wasim decide to strike a deal. In return for one Eclair from Alice, Wasim will help her complete her Maths homework which she has to submit tomorrow.

(Here we can see Wasim with Alice’s eclairs.)

But Wasim doesn’t know that Alice has yet to complete her English homework as well. Without telling Wasim, Alice has also made a secret deal with Bob. In return for one éclair from Alice, Bob would help Alice with her English homework. This deal is not known to anyone except Alice and Bob. Not Wasim and certainly not Ravi. And so, Alice has sent the same eclairs to Bob as well.

(Here we can see Bob with Alice’s Eclairs.)

Clearly, this is something that is not possible, right? This is known as “Double Spending”. It means that Alice is using the same eclairs to strike two deals. After she has already exhausted her eclairs, she is taking advantage of the fact that no one really knows about it. Let’s take this as Problem 3.

Why so Unfair?

Now then, we have three problems in our hands with no clear solution. Before we get to the solution, let’s look at one more story.

Let’s think of a place where we can keep the chocolates before sending them. Whenever someone wishes to send some chocolate to others, they have to send it to that place before it is sent to the intended person. This is actually how banks work. When Wasim send two gems to Bob, it would go first to the bank. Then the bank would send it to Bob.

(Two Gems sent through the bank.)

But here’s the curious thing, note how only one gem reaches Bob. Wasim sent 1 green and 1 red gem. The gems were sent to the bank first from where the gems were sent to Bob. But the bank takes one cut (here the green gem) out of the gems for its services and then sends the remaining gems to Bob.

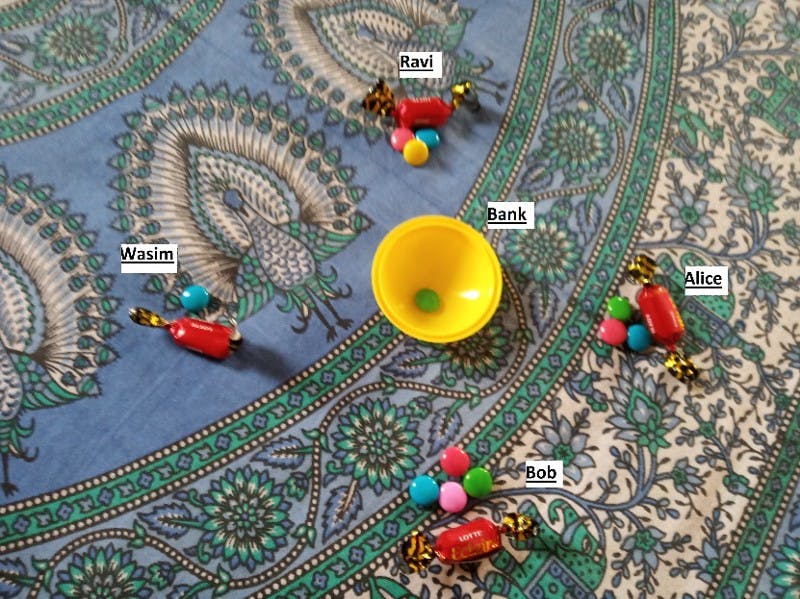
(Green gem remains with the Bank.)

If you look at the bank, it sounds fair, right? After all, they are giving Wasim this service so they are charging as well. But why should Wasim have to pay a charge out of the gems that he has earned? Could there not be a way to work around this? Let’s take this problem of the unfair cut as Problem 3.

Enter Blockchain — The Hero!

We now have three problems. Let’s summarize,

1. Problem 1 — Ravi shared one gem with Alice, but there was no proof of it. Alice ate the gem and told everyone she never received any gems from Ravi!
2. Problem 2 — Bob went on a quest and found an extra gem. He decided to use it unfairly and without anyone’s permission. According to him, he already had that gem from the beginning.
3. Problem 3 — Alice made 2 separate deals with Wasim and Bob using the same eclairs. Who owns the eclairs now? Or better yet, how can Alice use the eclairs once she has already given it to Wasim?
4. Problem 4 — Wasim sent two gems Bob with the help of Bank. But Bank kept one gem as payment for its services.

When we start, let’s say, Ravi, Alice, Bob, and Wasim each have a book. This book contains a record of everyone’s chocolate.

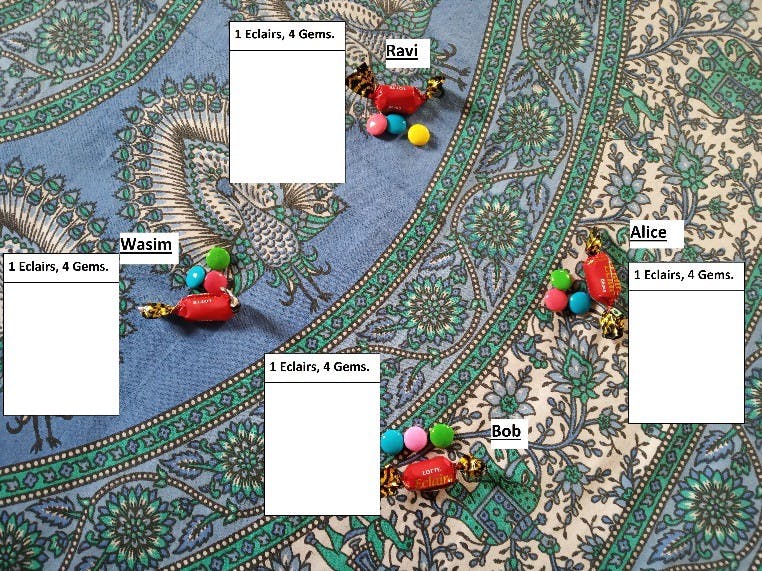
Everyone has a record. So let’s proceed.

When Ravi sends a gem to Alice, it is recorded on everyone’s book. This means that there are 4 proofs that Ravi did actually share a gem with Alice. So, now even if Alice gets hungry and eats the gem, she cannot claim that Ravi had not sent any gem to her. This solves Problem 1.

Next, Bob went on a quest and got 1 gem, right? He says that he had that from the beginning. But since everyone knows that was not the case, he is caught. Now, Bob can add this record to his book that he got this gem from a quest. This is also written in everyone’s books.

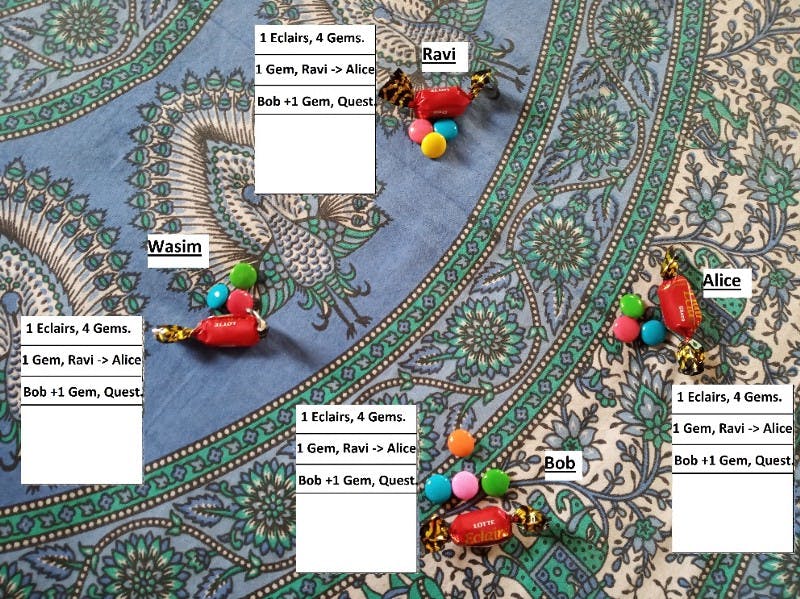
Simple as that. Everyone knows that Bob now has four gems and 1 Eclair. This solves Problem 2.

After this, we see that Alice did a “double spending” with the eclairs she had. How does this book solve that problem? Let’s see.

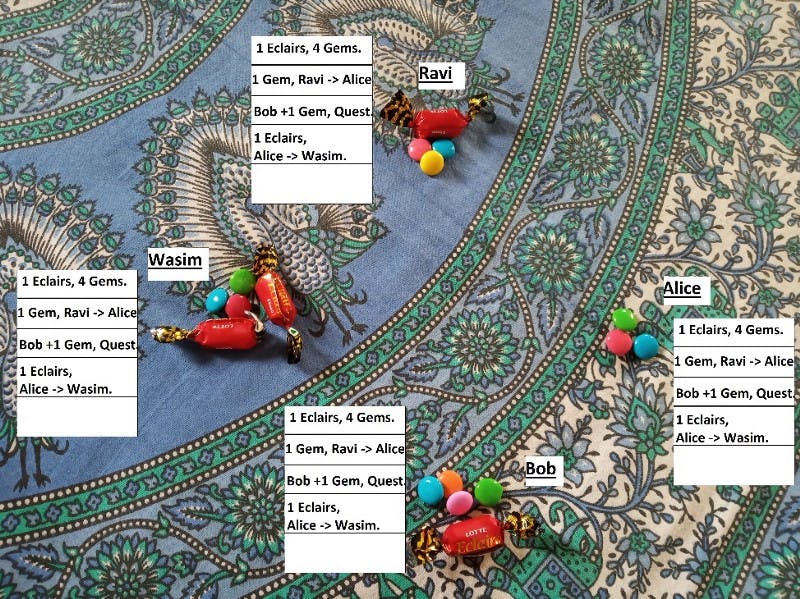
When Alice gives Wasim the eclairs she had in return for her homework, everyone records that their books. So, the next time Alice tries to send Eclairs to Bob in return for English Homework, everyone checks their books.

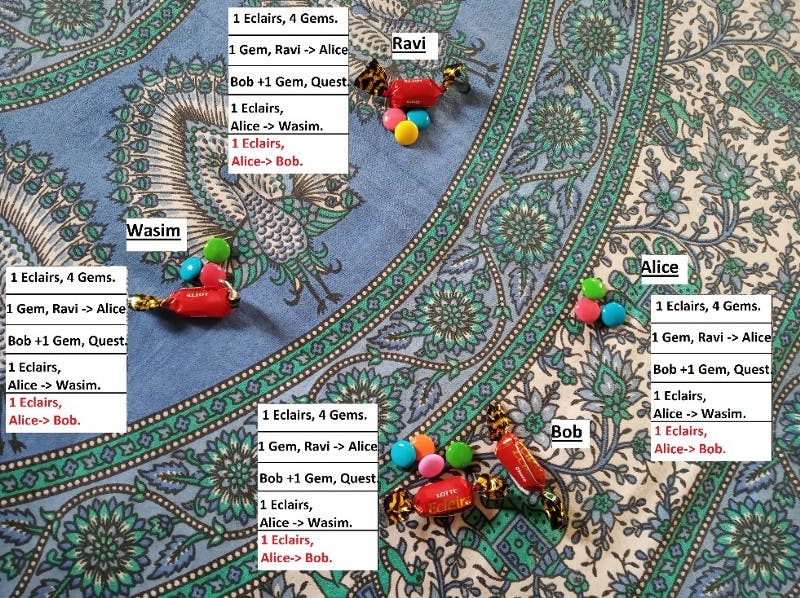
Bob, Wasim and Ravi find that Alice does not have an Eclairs she can send to Bob in the first place. Hence, she cannot make this deal. Thus, “double spending” cannot take place and Problem 3 is solved.

This just leaves out Problem 4, right? Well, take a good look at where we are. The solution to Problem 4 is here already. Did you spot it?

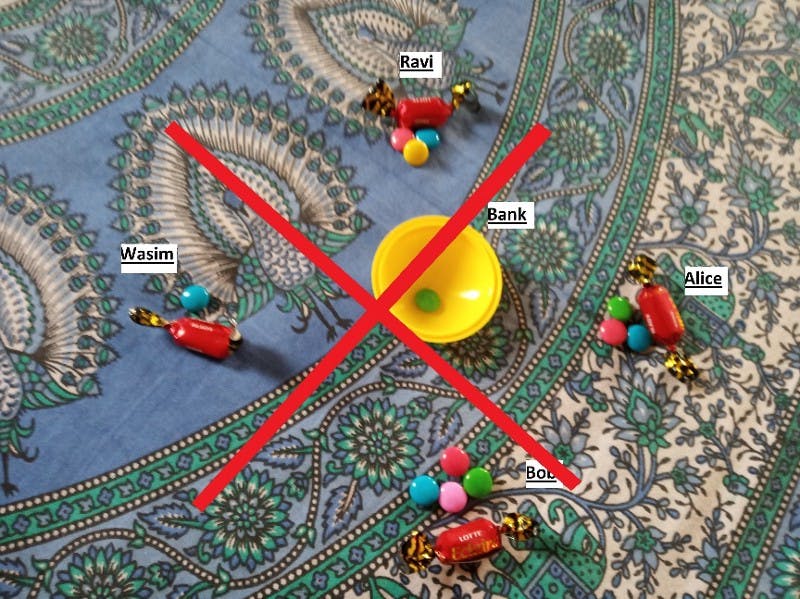
Now, if you note, everyone is recording the gems and eclairs in their books. They all can see each other’s books. There is no need for a Bank in this case, right? The purpose of the bank is served. So the next time Wasim sends Bob 2 gems, no one will take any cut from it. This solves Problem 4.

But What is the Blockchain?

Remember this little piece of thing? We were calling it a “book”. This is where everyone’s actions were being recorded. And every one of the friends, Ravi, Bob, Alice, and Wasim had a copy of it. Every action was being checked first and then recorded once every one of them reached a decision.

Turns out, this becomes a “block” and multiple such blocks make up the Blockchain which every participant has a copy of. Surprising, right?

One way to understand it is by taking every action in the list (“1 Eclairs, 1 Gem”, “1 Gem, Ravi -> Alice” and so on) these can be thought of as blocks if you want to. And this whole list is like a chain of these blocks, right? You might think of it like this as well.

This is the Blockchain (well a trimmed down version of it at least). In the real world, this is used to record hundreds and thousands of such actions between two or more friends. As you can easily see, this makes it all “transparent” and improves “trust” between the friends (Ravi, Bob, Alice, and Wasim). Moreover, if say someone was trying to do something naughty, such as changing the list, he or she would have to change all the four copies of it at once. This is very difficult, wouldn’t you say? Which means the friends are safe and secure! (It might not seem so difficult here, but imagine a group of 100 or 1000 friends, each of them with their own copy)

And that’s it. That’s what Blockchain is and how helpful it can be. Hope you enjoyed it!

Take Care!